'분류 전체보기'에 해당되는 글 1250건

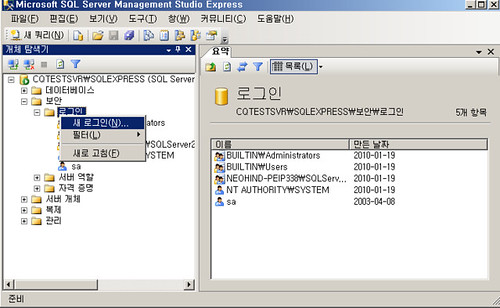
DAMO(Domino Access for Microsoft Outlook) 프로그램을 사용하여,

Outlook에서도 마치 Exchange 쓰듯 Lotus Domino 서버를 활용할 수 있다.

보통 XP의 Outlook 2003에서는 상당히 제정신으로 도는데,

MS에서도 밥벌어먹고 살려면 업그레이드를 해야 되겠고,

결국 덩달아 업그레이드를 하다 보니, 현재 구성은 Windows 7에 Outlook 2007이 되버렸다.

그러나 최적의 환경을 구성하기에는 너무 구닥다리 같은 UI와 기능들에

결국 꿋꿋하게 Windows 7의 Outlook 2007을 활용하려고 한다.

그러나 현재 Outlook 2007을 종료하면 자꾸 프로그램 오류가 발생한다.

에러 내용은 아래와 같다.

Faulting application name: OUTLOOK.EXE, version: 12.0.4518.1014, time stamp: 0x4542840f
Faulting module name: nwnspR32.dll_unloaded, version: 0.0.0.0, time stamp: 0x489c864f
Exception code: 0xc0000005
Fault offset: 0x01e82e74
Faulting process id: 0xcf4
Faulting application start time: 0x01ca9e6097aafc8d
Faulting application path: C:\Program Files\Microsoft Office\Office12\OUTLOOK.EXE
Faulting module path: nwnspR32.dll
Report Id: f39a9d85-0a53-11df-b241-001f3b661b0f

일단 현재까지 파악한 내용은 Windows 7(Vista 때 부터 담겼던) Windows Search가 Outlook 자원까지 찝적거린결과 였었다. 최소한 Windows Search가 찝적되면 Outlook이 제대로 작동하지 않는다.

이 것을 해결하는 방법은 아래의 레지스트리를 수정하면 된다.( 대개는 없으므로 추가해야 한다. )

[HKEY_LOCAL_MACHINE\SOFTWARE\Policies\Microsoft\Windows\Windows Search]
"PreventIndexingOutlook"=dword:00000001

그리고 난 뒤, Windows Search 서비스를 재 시작하거나, 아니면 컴퓨터를 리부팅 한다.

UPDATE: 2010-01-06 18:41

SP1을 적용했으나, 변화 없음 똑 같은 형태로 에러가 발생한다.

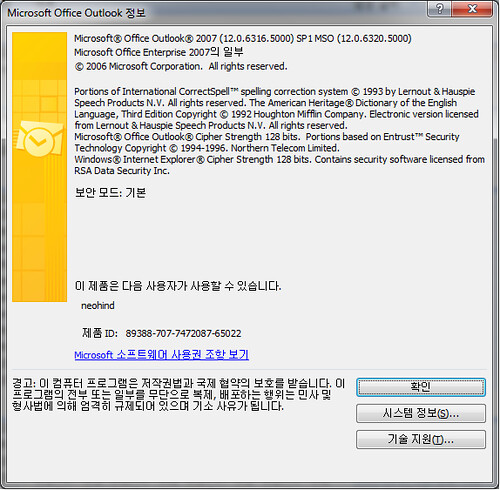
현재 설치된 버전의 About 내용은 아래와 같다.

   Outlook 2007

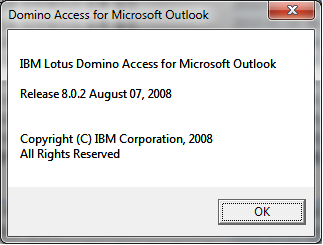
  DAMO 8.0.2

일단 현재 상황은 아직도 오류는 발생 오류 내용은 아래와 같다.

Faulting application name: OUTLOOK.EXE, version: 12.0.6316.5000, time stamp: 0x4833a470
Faulting module name: nwnspR32.dll_unloaded, version: 0.0.0.0, time stamp: 0x489c864f
Exception code: 0xc0000005
Fault offset: 0x02222e74
Faulting process id: 0x5d4
Faulting application start time: 0x01ca9e6b2826f17f
Faulting application path: C:\Program Files\Microsoft Office\Office12\OUTLOOK.EXE
Faulting module path: nwnspR32.dll
Report Id: c4be8a8d-0a5e-11df-9165-005056c00008

짐작이지만, Outlook 종료 때, 이 DAMO의 핵심 DLL인 nwnspR32.dll 이 지연되서 발생되는 문제같다. 아무래도 Notes와의 연결을 정리해야 하는데, 그 시간이 의외 많이 걸리는듯...

Outlook이 조금 천천히 종료되거나, 이 DAMO가 빨리 종료되면 문제가 없을 것 같은데...

역 어셈블해서 까야 되나... 일단 SP2를 한번 받아서 설치해보고 그 뒤를 보도록 하겠다.

원본글 : http://code.google.com/appengine/docs/java/gettingstarted/usingusers.html

Google App Engine에서는 Google 인프라 스트럭처를 활용한 몇몇 유용한 서비스를 제공합니다.

이 서비스들은 SDK에 포함된 라이브러리를 이용하여 응용 프로그램에서 접근 가능합니다.

Users Service와 같은 서비스는 Google 사용자 계정과 통합되어 여러분들의 응용 프로그램에서 활용할 수 있습니다. 그래서 응용 프로그램 내에 Google 계정을 이용해 가입된 사용자들의 정보를 활용할 수 있습니다.

이제부터 Users service를 이용하여, 개별 사용자 별로 인사말이 표시되게 끔 하는 방법을 구현하려 합니다.

Users 사용하기.

src/guestbook/GuestBookServlet.java를 편집하여 열어보면 다음과 같습니다.

package guestbook;

import java.io.IOException;
import javax.servlet.http.*;
import com.google.appengine.api.users.User;
import com.google.appengine.api.users.UserService;
import com.google.appengine.api.users.UserServiceFactory;
public class GuestbookServlet extends HttpServlet {
    public void doGet(HttpServletRequest req, HttpServletResponse resp)
              throws IOException {
        UserService userService = UserServiceFactory.getUserService();
        User user = userService.getCurrentUser();

        if (user != null) {
            resp.setContentType("text/plain");
            resp.getWriter().println("Hello, " + user.getNickname());
        } else {
            resp.sendRedirect(userService.createLoginURL(req.getRequestURI()));
        }
    }
}

원본글 : http://code.google.com/appengine/docs/java/gettingstarted/creating.html

App Engine Java 응용 프로그램은 Java 서블릿 표준을 이용하여 웹 서버 환경과 연동합니다.

컴파일 된 클래스, JAR, 정적 파일 및 설정 파일들을 포함한 응용 프로그램 파일들은

WAR 라는 자바 웹 응용 프로그램 표준 Layout을 이용하여 디렉터리 별로 정리되어 저장되게 됩니다.

이 WAR 디렉터리 구성은 다른 어떤 Java 웹 응용 프로그램 구성에서도 동일하게 적용됩니다.

( 애석하게도 SDK 에서는 이 WAR 저장 방식 파일에 대해서 지원되지 않습니다. )

프로젝트 디렉터리

현재 이 튜토리얼에서는 모든 프로젝트 파일들은 Guestbook/이라는 이름으로 된 단 하나의 디렉터리 안에 담겨 있습니다. src/ 라는 하위 디렉터리에는 Java 소스 코드들이 담겨 있으며, war/ 라는 하위 디렉터리에는 WAR 포맷에 맞게 구성된 응용 프로그램들이 담겨 있습니다.

Java 소스 파일들이 컴파일 되면 war/의 위치에 컴파일 된 파일들이 담기게 해야 합니다.

완전한 프로젝트 디렉터리는 다음과 같은 형태가 되어 있어야 합니다.

Guestbook/
  src/
    ...자바소스 파일들...
    META-INF/
      ...기타 설정 파일들...
  war/
    ...JSPs, 이미지, 데이터 파일...
    WEB-INF/
      ...응용 프로그램 설정 내용...
      lib/
        ...라이브러리 JAR들...
      classes/
        ...컴파일된 클래스들...

Eclipse 에서는 툴바에서 New Web Application Project 버튼()을 클릭하여 새로운 프로젝트를 생성하기만 하시면 됩니다. 새 프로젝트에 대한 설정 창에서 “Project Name”에는 Guestbook 을, “Package”에는 guestbook 을 넣어주시고 “Use Google Web Toolkit”의 체크를 풀어주시고, 대신 “Use Google App Engine”에 체크해주시기 바랍니다. 그러면 Eclipse의 Plugin에서 제공하는 마법사를 통해 위에서 언급한 디렉토리 구조를 구성하고 필요한 기본적인 파일들을 배치하게 됩니다.

SDK안에 포함된 새 프로젝트 템플릿을 직접 복사해서 구성하실 수도 있습니다.
이 템플릿은 appengine-java-sdk/demos/new_project_template/ 디렉터리에 위치해 있습니다.

서블릿 클래스

App Engine Java 응용 프로그램에서는 the Java Sevlet API를 이용하여 웹 서버와 직접적인 연결을 합니다. HTTP 서블릿은 응용 프로그램 클래스로 웹에서의 요청에 대한 응답 프로세스를 할 수 있습니다.
이런 요청 응답용 클래스는 javax.servlet.GenericServlet 클래스

또는 javax.servlet.http.HttpServlet 클래스를 상속 받은 클래스로 구성하게 됩니다.

예제로 구성된 방명록 프로젝트는 하나의 서블릿 클래스로 시작되어 있으며

단순한 서블릿을 사용하여 메시지를 출력하게 됩니다.

이 파일은 src/guestbook/ 디렉터리에 GuestbookServlet.java 파일로 다음과 같이 구성되어 있습니다.

package guestbook;

import java.io.IOException;
import javax.servlet.http.*;

public class GuestbookServlet extends HttpServlet {
    public void doGet(HttpServletRequest req, HttpServletResponse resp)
            throws IOException {
        resp.setContentType("text/plain");
        resp.getWriter().println("Hello, world");
    }
}

web.xml 파일에 대해

웹서버에서 요청을 받았을 때, 서블릿 클래스에서는 “웹 응용 프로그램 배치 설명자(web application deployment descriptor)” 라고 불리는 구성 파일을 사용하여 요청된 서블릿 클래스을 선택하게 됩니다.

이 파일은 보통 web.xml 이라고 이름 지어지며, WAR 파일 안에 있는 war/WEB-INF/ 디렉토리에 담기게 됩니다. WEB-INF/ 와 web.xml은 서블릿 규칙에 따라 이름 지어지고 위치된 것입니다.

war/WEB-INF/ 디렉토리에 있는 web.xml 내용을 대략적으로 보면 다음과 같습니다.

<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE web-app PUBLIC
 "-//Sun Microsystems, Inc.//DTD Web Application 2.3//EN"
 "http://java.sun.com/dtd/web-app_2_3.dtd">

<web-app xmlns="http://java.sun.com/xml/ns/javaee" version="2.5">
    <servlet>
        <servlet-name>guestbook</servlet-name>
        <servlet-class>guestbook.GuestbookServlet</servlet-class>
    </servlet>
    <servlet-mapping>
        <servlet-name>guestbook</servlet-name>
        <url-pattern>/guestbook</url-pattern>
    </servlet-mapping>
    <welcome-file-list>
        <welcome-file>/index.html</welcome-file>
    </welcome-file-list>
</web-app>

Eclipse에서 해당 XML을 열면 아래와 같이 보입니다.

이 web.xml 파일은 서블릿인 guestbook에 대한 선언을 담게 되며,

/guestbook 이라는 URL path와 연결되게 끔 구성하는 것을 보여주고 있습니다.

응용 프로그램의 WAR 안에 디렉토리 경로 상에서 없는 경로를 이용하여 서브릿과 연결하여,

외부에서는 전혀 다른 형태의 URL로 접근할 수 있도록 해줍니다.

하지만, 해당 하는 경로에 index.html 이 있다면, 서블릿 설정보다 index.html을 먼저 보여주게 됩니다.

appengin-web.xml 파일에 대해

App Engine은 추가적은 설정 파일이 하나 더 있습니다.

이 파일은 응용 프로그램을 어떻게 배포하고, 실행할지에 대해서 나타내는 설정 파일입니다.

반드시 이 파일은 web.xml 이 있는 WEB-INF/ 디렉토리 안에 위치해야 하며,

그 이름은 appengine-web.xml 이여야 합니다.

그 안에는 응용 프로그램의 등록 ID( Eclipse에서는 언제든지 채울 수 있도록 빈 ID를 생성하여 제공합니다. ), 정적 파일(이미지나 CSS 등등), 리소스 파일(JSP 파일이나, 기타 응용 프로그램 데이터)과 같이 명시적으로 나타낼 내용들을 담고 있습니다 .

war/WEB-INF/ 디렉터리 안에 있는 appengine-web.xml 이라는 파일은 다음과 같이 되어 있습니다.

<?xml version="1.0" encoding="utf-8"?>
<appengine-web-app xmlns="http://appengine.google.com/ns/1.0">
    <application></application>
    <version>1</version>
</appengine-web-app>

appengine-web.xml 에는 App Engine에 대해 설명하는 내용을 담고 있지만,

서블릿 표준에 포함되는 내용은 아닙니다.

SDK에 보시면 이 파일의 형식에 대해 명기되어 있는 XML 스키마 파일을

appengine-java-sdk/docs 안에서 찾을 수 있습니다.

이 파일에 대한 자세한 설명은 Configuring an App를 보시기 바랍니다.

프로젝트 실행하기.

App Engine SDK 에는 여러분이 만든 응용 프로그램을 테스트 할 수 있도록

제공되는 웹서버 응용 프로그램을 포함하고 있습니다.

이 서버는 sandbox 제약영역, 저장소, 기타 서비스 등

각종 App Engine 환경에서 제공되는 기본적인 기능들을 모두 제공합니다.

이 웹서버는 Eclipse의 Debugger로 간단하게 시작할 수 있습니다.

Run 메뉴 안에 있는 Debug As > Web Application을 선택하기만 하면 됩니다. 

디버그 관련된 설정 방법은 Google Plugin in Eclipse 사용하기를 참고하시기 바랍니다.

응용 프로그램 테스트 하기.

서버가 시작되면, 여러분의 브라우저를 이용하여 다음 URL을 입력해보시기 바랍니다.

http://localhost:8080/guestbook

(간혹 설정 상으로 http://localhost:9999/guestbook 일 수도 있습니다. 
  포트 번호는 각자 확인해보시기 바랍니다. )
서버에서 서블릿을 호출하면, 브라우저 상에 메시지를 출력할 것입니다.

다음은…

여기 까지 오셨다면 기본적인 App Engine 응용 프로그램을 성공적으로 제작하신 것입니다!.
이제 이 내용을 배포만 하시면 전세계의 모든 사용자들과 권리를 누리며 나누실 수 있습니다.
이 응용 프로그램은 모든 사용자에 대한 일반적인 인사 내용을 보여줍니다.

이제부터는 인사말을 커스터마이징 하여,

Google Account로 접속한 사용자들에 대한 별도의 인사말을 만들어보도록 하겠습니다.

다음은, User Service를 사용하기 에서 계속 됩니다.

성격
	다재 다능한 재주꾼이다. 이 성좌에 출생한 사람은 재치 있고 연설에 능하며 문장력도 뛰어나다. 여러 방면에 걸쳐 재능이 풍부하여 어떤 일을 막론하고 일단 착수하기 시작하면 일에 대한 보답이나 이해 관계를 초월해서 온 정성을 다해 그 일을 해내고 만다. 그러나 능력만큼 대우를 받지 못하고 또 능력을 제대로 발휘할 수 있는 환경이 마련되지 않아 삶에 대한 불만이 크다. 모든 재주꾼이 그러하듯이 천부적인 재능으로 인해 꿈이 크고 이상이 원대하여 어떤 일이든 자신만만하게 해낼 수 있다는 자부심을 가지면서도 운명에 대해서는 회의를 느껴 자칫 타락하기도 쉽다. 간혹 염세주의자들이 있다. 뿐만 아니라 사회에 대한 저항감이 강하여 군중을 선동하는가 하면 납의 결점이나 정치적 비판 등을 능란한 연설로 전개한다. 마음을 닦고 안정하여 학문이나 예술 방면에 진력한다면 상당한 명성을 얻을 수 있는 인재이다. 적합한 직업으로는 문인, 탤런트 등이 있다.
연애와 결혼
	쌍 둥이좌 태생은 열렬한 사랑에 빠지는 법이 없다. 그것을 회피해서가 아니라 이성에 냉담한 편이어서 평소 자기가 꿈꾸던 완전한 이상형이 아니면 또 다른 이성을 사랑할 수 있는 빈 자리를 남겨 두기 때문이다. 이성 교제를 함에 좋아한다는 것과 사랑한다는 것의 한계가 분명하여 좋아는 할지언정 사랑하기에는 어딘가 밑진다는 생각을 늘 하고 있다. 세상에는 완전한 사람이 있을 수 없는 것이므로 쌍둥이좌 출생의 주인공은 사랑에 흠뻑 빠져버리지 못하는 불행한 사람이다. 흔히 말하기를 이성에 반해 버리면 결점도 아름답게 보인다고 하는데 쌍둥이 좌의 눈에는 그것이 통하지 않고 아무리 좋아해도 결점은 결점 그대로 보여 한 구석에 꺼림칙한 마음을 갖고 있다. 쌍둥이좌의 남성은 지성미와 남성적인 풍모가 있어 많은 여성들이 좋아하게 되지만 냉정한 면이 있어 접근하기가 어렵다. 이성교제를 절실히 원하면서도 자존심을 굽히면서까지 구애하기가 싫어 망설이다가 어떤 여성이 용감하게 접근해 오면 다행으로 여겨 쉽게 받아들이지만 다만 다른 상대가 나타나면 이중·삼중적인 연애를 한다. 그러나 이 주인공의 바람기란 무리가 없는 한계에서 행하는 것으로 상대방을 불행으로 빠뜨린다거나 결혼생활이 파괴될 정도에 이르지는 않는다. 여성도 애정관이 남성의 예와 비슷하다. 설사 육체를 허락한 남성이라도 그에게 흠뻑 빠진다거나 매달리는 일이 없이 냉철하게 자기 자신으로 돌아오곤 한다. 그래서 쌍둥이 좌의 여성은 좋아하는 남성과 키스를 하고 있으면서도 거기에 완전히 도취되지 못하고 무엇인가 딴 생각을 하거나 상대방 남성의 못마땅한 점을 생각하게 된다. 결혼한 뒤에는 본시 타고난 성품 이 냉철하므로 극단적인 불행에까지 이르지는 않으나 자기의 남편과 다른 남편을 비교하는 버릇이 있어 애정이 있어서라기보다는 의무감으로 그런 대로 평탄한 가정을 유지해 나간다. 만약 이 성좌의 여성이 완전한 이상형의 남성과 결혼한다면 자신의 모든 것을 바쳐 남편을 사랑하고 남편을 위해 희생할 것이다.
결혼상대
	물병좌(1월 21일∼2월 19일), 천칭좌(9월 24일∼10월 23일), 사수좌(11월 23일∼12월 22일) 출생과 만나면 원만한 가정을 이룬다

1. SQL 내 DB 만들기.

• 제일 먼저, Windows 통합 인증을 쓰던, SQL 인증방식을 쓰던, DB Admin 급의 계정으로 일단 SQL Express에 접속한다. 뭐 이 접속이 바로 Management Studio를 의미한다는 사실은 당연한 것.
• 그리고 개체 탐색기의 트리를 열어 보안 > 로그인 부분에서 오른쪽 버튼 클릭. 컨텍스트 메뉴에서 새 로그인(N)... 을 선택.
  
• 계정을 만든다. 여기서는 그냥 cqadmin 이라고 했다. 다음 부분이 중요한데, 반드시 SQL Server 인증을 선택하고, 암호를 넣어준다. 또한 "암호 정첵 강제 적용(F)"을 반드시 끈다. 이거 켜면, 대부분 SQL 서비스를 사용하는 제품들은 제대로 동작하는 걸 본적이 없다. (닷넷으로 만든 제품은 설정 조금 바꾸면 되기는 하지만, C/C++ 로 만든 제품은 저 기능에 대응하려면 SQL 접속 모듈을 다시 만들어야 됨 -_-;;;;; ) 아래 화면 처럼 되었다면 확인! 하여 저장.
  
• cqadmin 계정 생성을 성공했다면, 이번엔 CQ의 스키마를 저장하기 위한 DB를 만들도록 한다. 만드는 방법은 개체 탐색기 트리에서 데이터베이스 위에서 오른쪽 버튼 클릭! 컨텍스트 메뉴에서 새 데이터베이스(N)을 선택한다.
  
• 새 데이터베이스의 속성들을 결정하는 부분에서 먼저 DB 이름을 넣어준다. ( 아직 확인은 누르지 마세요!!! )
  
• 이제 왼쪽 트리 중 옵션에 들어간다. 핵심부분으로 꼭 이 부분을 확실하게 체크해야 한다. 반드시 데이터 정렬에서 "Korean_Wansung_CI_AS"를 선택하도록 한다. 물론 이 부분은 실제 CQ에서 언어코드에 따라 달라지게 된다. 만일 중국어라면, 코드가 936 인데, 이런 경우 "Chinese_PRC_CI_AS"를 선택하면 된다. 자세한 언어 코드별 정렬 방법에 대한 정보는 설치 프로그램에서 데이터 정렬 설정 부분을 참고하도록 한다. 나머지 설정은 그대로 두고 "확인"을 클릭해 저장한다.
  
• 자 이제는 새로 만들어진 DB에 대한 보안 설정을 해야 한다. 즉 앞서 만든 계정인 cqadmin을 이 DB와 연결해야 한다. 여기서는 단 한가지만 주의하면 되는데, cqadmin에게 db_owner에 대한 스키마 소유권을 안 주는게 핵심. 왜 그런지는 아직 파악을 못했지만, 최소한 CQ가 SQL 2005에 접속할 때, cqadmin이라는 계정이 db_owner의 소유권이 있는 경우 DB에 제대로 접속을 못하는 문제가 발생한다. 이 부분을 반드시 체크하고 넘어갈 필요가 있다. 사설이 길어졌는데, 하는 방법은 다음과 같다.
• 다시 화면이 떴을때, 왼쪽 개체 탐색기 트리에서 이번엔 새로 만든 DB 아래를 펼쳐서 보안의 사용자 단계까지 간다. 즉 데이터베이스 > cqschema > 보안 > 사용자 까지 내려 온다. 사용자 부분에서 오른쪽 버튼 클릭!. 컨텍스트 메뉴에서 새 사용자(N) 을 선택해 준다.
  
• 자 신규 사용자 정보를 넣는 창이 나오는데, 여기서 다음과 같이 입력한다. 사용자 이름/로그인 이름/기본 스키마에 앞서 만든 계정인 cqadmin으로 다 때려 넣는다. 그리고 중요한거!!! 소유한 스키마는 절대 손대지 마시고! 대신 데이터베이스 역할 맴버 자격안에 db_owner를 선택한다. 나머지 옵션을 그냥 두고, 확인을 클릭하여 저장한다.
  
• 예전에는 자동으로 만들어졌던 거 같은데, 이상하게 자동으로 잘 안만들어지는게 기본 스키마. 위에서 설정에서 새롭게 지정한 cqadmin 스키마를 만들어주어야 한다. 만드는 방법은 간단. 개체 탐색기에서 아까 열었던 사용자 부분 아래 아래 보면 스키마가 있는데, 거기서 오른쪽 버튼 클릭!!!! 그리고 컨텍스트 메뉴에서 새 스키마(N)을 선택하면 된다.
  
• 썰렁한 창안에 앵무새 떠들듯 계정을 그대로 넣어주면 된다. cqadmin, cqadmin.. 그리고 확인을 눌러 저장한다.
  
• 자!!! DB 준비는 끝.. 이제 ClearQuest 유지보수 도구를 실행한다.

• 화면이 떴으면 Create를 클릭한다.
  
• 자 그러면 스키마 연결을 위한 이름이 기본값으로 설정되고(스키마가 아무것도 없었다면 7.0.0) 스키마 저장소에 대한 설정 값을 입력하게 된다.  각 해당하는 값을 아래와 같이 입력한다.    
  - Feature Level : FEATURE_LEVEL_7 
    ( 만일 기존 7.0.1에서 백업한 데이터를 사용한다면, LEVEL_6을 선택한다. )    
  - Physical Database Name : cqschema  
    ( 앞서 만든 DB 이름을 넣는다. )    
  - Database Server Name : CQTESTSVR\SQLEXPRESS
    ( 이 이름 모르겠다면 SQL Management Studio 접속 화면에서 확인하시면 된다.)    
  - Administrator Name : cqadmin
    ( 앞서 만든 계정 )    
  - Administartor Password : ***** 
    ( 계정에 해당하는 암호)   
  - Connect Option :               
    (그냥 비우면 됨!)
  다 입력했으면 다음(N)을 클릭한다.
  
•  언어코드는 한국어 이니 949 그대로 두고 다음!
•  자동으로 Sample Database를 만들겠냐는 질문인데, 그냥 체크를 끄자. 만들 필요 없다. 다 되었다면 마침을 클릭한다.
• 그러면 자동적으로 DB 설정을 시작한다.그러면 Status 창에 무언가 주저리 주거리 많은 로그들이 남다가,
  완료되면 Done 버튼이 활성화 된다. 이제 Done만 누르면 완료된다.